Tree structure (struktur pohon) sangat umum ditemui. Mulai dari struktur
folder/direktori di komputer Anda, sampai di setiap halaman web yang Anda
kunjungi (dokumen HTML memiliki struktur tree, setiap browser ada struktur tree
untuk DOM HTML). Beberapa contoh lain di mana Anda akan menemui struktur pohon:
- Memproses XML memerlukan pemahaman mengenai tree
- Pohon keluarga (family tree)
- Pohon organisasi
- Membuat pivot table yang kompleks memerlukan pemahaman mengenai tree
Jika Anda menjadi administrator
database yang ingin bisa mengoptimasi sampai level penyimpanan, Anda harus tahu
struktur dasar seperti B-tree. Di beberapa database, misalnya Oracle, Anda bisa
mengatur ukuran blocksize untuk indeks B-tree.
Struktur graph (graf) juga
banyak digunakan sehari-hari:
- Node-node dalam sebuah jaringan membentuk graf, dan ini perlu dipahami oleh administrator jaringan.
- Jalan dan lokasi di sebuah peta bisa dianggap sebagai graf.
- Jaringan pertemanan (di Facebook, Friendster, dsb) juga merupakan graf. Jika Anda membuat situs seperti itu, Anda perlu tahu konsep graf.
Ada beberapa gabungan dari tree dan
graph. Jika Anda menjadi administrator jaringan, Anda perlu mengenal konsep
spanning tree untuk mengkonfigurasi STP (spanning tree protocol). Jika Anda
perlu membuat program peta sendiri, Anda perlu struktur data quad-tree untuk
mengakses dengan cepat node-node dalam graf yang Anda miliki.
Mungkin sebagian dari Anda berpikir:
itu kan hanya sebagian saja struktur data yang ada, bagaimana dengan yang lain?
Ketika belajar struktur data yang
sederhana akan membantu kita memahami struktur data yang lebih kompleks.
Misalnya jika seseorang tiba-tiba diminta mengimplementasikan tree dengan
pointer, dia biasanya akan bingung. Sementara jika diajari selangkah demi
selangkah mulai dari linked list, maka biasanya akan lebih mudah. Jadi fungsi
pertama struktur yang sederhana adalah untuk mempelajari struktur yang lebih
rumit. Dalam berbagai bahasa, struktur Linked List, Double Linked List, dsb
sudah masuk menjadi API standar.
Dalam mengimplementasikan suatu
struktur data, Anda bisa melihat kelebihan dan kekurangan masing-masing
struktur data. Misalnya linked list sangat efisien untuk menyimpan data yang
selalu ditambahkan di akhir. Ini akan membantu Anda memilih struktud data
terbaik untuk keperluan Anda (jadi Anda tidak selalu hanya memakai
java.util.Vector saja di Java). Jadi penggunaan struktur data spesifik berguna
untuk optimasi.
Misalnya Anda punya beberapa punya
struktur data yang hanya selalu ditambah saja di akhir. Struktur List akan
sangat efisien untuk hal ini. Jika Anda sudah tahu tepatnya berapa data yang
akan datang Anda bisa memakai array (atau std::vector di C++, atau
java.util.Vector di Java). Tapi jika Anda tidak tahu, setiap kali array mencapai
kapasitasnya, Anda perlu meresize memori (dan jika ternyata memori tidak cukup,
tanpa sepengetahuan Anda kadang perlu ada penyalinan data ke lokasi memori yang
baru). Jadi dalam kasus ini Anda bisa melihat bahwa List sederhana juga punya
kegunaan.
Kesimpulannya adalah: mempelajari
struktur data merupakan hal yang penting. Hanya di bidang yang sangat sempit
saja kita tidak perlu mempelajari struktur data. Dan bahkan dalam bidang yang
sempit itu, pemahaman struktur data akan bisa banyak membantu untuk membuat
program yang lebih baik.
STRUKTUR DATA QUEUE
Queue (antrian) adalah struktur data
dimana data yang pertama kali dimasukkan adalah data yang pertama kali bisa
dihapus. Atau bisa juga disebut dengan struktur data yang menggunakan mekanisme
FIFO (First In First Out). Queue dalam kehidupan sehari-hari seperti antrian
pada penjualan tiket kereta api, dimana orang yang pertama datang adalah orang
yang pertama kali dilayani untuk membeli tiket.
Jika ada orangbaru yang datang akan
membali tiket, maka posisinya berada pada urutan paling belakang dalam antrian
tersebut. Orang yang berada pada posisi terakhir dalam antrian adalah yang
terakhir kali dapat dilayani dan memperoleh tiket kereta api (kalau kurang
beruntung, maka akan kehabisan tiket). Contoh lain adalah nasabah yang antri di
teller bank, paket data yang menunggu untuk ditransmisikan lewat internet,
antrian printer dimana terdapat antrian print job yang menunggu giliran untuk
menggunakan printer, dsb. Istilah-istilah yang digunakan dalam queue (antrian)
Memasukkan data (insert) disebut juga dengan put, add, atau enqueue. Menghapus data (remove) biasa disebut dengan istilah delete, get, atau dequeue. Bagian belakang queue, dimana data bisa dimasukkan disebut dengan back, tail (ekor), atau end (akhir). Sedangkan bagian depan (front) queue dimana data bisa dihapus juga biasa disebut dengan istilah kepala (head).
Memasukkan data (insert) disebut juga dengan put, add, atau enqueue. Menghapus data (remove) biasa disebut dengan istilah delete, get, atau dequeue. Bagian belakang queue, dimana data bisa dimasukkan disebut dengan back, tail (ekor), atau end (akhir). Sedangkan bagian depan (front) queue dimana data bisa dihapus juga biasa disebut dengan istilah kepala (head).
Circular Queue
Di dunia nyata apabila seseorang sedang mengantri (misalnya antri tiket kereta api), apabila telah dilayani dan memperoleh tiket, maka ia akan keluar dari antrian dan orang-orang yang berada di belakangnya akan bergerak maju ke dapan. Kita bisa saja menggerakkan setiap item data ke depan apabila kita menghapus data yang terdepan, tetapi hal ini kurang efektif. Sebaliknya kita tetap menjaga setiap item data di posisinya, yang kita lakukan hanyalah merubah posisi front dan rear saja.
Yang menjadi permasalahan adalah apabila posisi rear berada pada bagian akhir dari array (atau pada nomor indeks yang terbesar). Meskipun ada bagian yang kosong di awal-awal array – karena mungkin data telah dihapus, data baru tidak bisa dimasukkan lagi karena rear-nya sudah tidak bisa bergerak lagi. Atau mungkinkah posisi rear nya bisa berpindah? Situasi seperti itu bisa dilihat seperti gambar berikut:
circular queueUntuk menghindari permasalahan seperti itu (tidak bisa memasukkan data baru) – meskipun queue-nya belum penuh, maka front dan rear-nya berputar (kembali) ke bagian awal array. Kejadian seperti ini dinamakan dengan circular queue (atau kadang-kadang disebut juga dengan istilah ring buffer). Kejadian seperti ini seperti terlihat pada gambar berikut:
Berikut Contoh Implementasi Antrian dalam Java :
Queue.java
class Queue
{
private int maxSize;
private long[] queArray;
private int front;
private int rear;
private int nItems;
//————————————————————–
public Queue(int s) // konstruktor
{
maxSize = s;
queArray = new long[maxSize];
front = 0;
rear = -1;
nItems = 0;
}
//————————————————————–
public void insert(long j) // letakkan item (data) di posisi belakang dari queue
{
if(rear == maxSize-1) //
rear = -1;
queArray[++rear] = j; //naikkan rear dan masukkan item (data) pada posisi rear yang baru
nItems++; //tambah satu item lagi
}
//————————————————————–
public long remove() // hapus item (data) yang berada pada posisi front
{
long temp = queArray[front++]; //dapatkan nilainya dan naikkan front
if(front == maxSize) //
front = 0;
nItems–; // item (data) berkurang satu
return temp;
}
//————————————————————–
public long peekFront() //
{
return queArray[front];
}
//————————————————————–
public boolean isEmpty() //benar jika queue-nya kosong
{
return (nItems==0);
}
//————————————————————–
public boolean isFull() // benar jika queue-nya penuh
{
return (nItems==maxSize);
}
//————————————————————–
public int size() // jumlah ietm (data) dalam queue
{
return nItems;
}
//————————————————————–
} // end class Queue
QueueApp.java
class QueueApp
{
public static void main(String[] args)
{
Queue theQueue = new Queue(5); // queue menampung 5 item (data)
theQueue.insert(10); // masukkan 4 item (data)
theQueue.insert(20);
theQueue.insert(30);
theQueue.insert(40);
theQueue.remove(); // hapus 3 item (data)
theQueue.remove(); // (10, 20, 30)
theQueue.remove();
theQueue.insert(50); // masukkan 4 item (data) lagi
theQueue.insert(60); // (wraps around)
theQueue.insert(70);
theQueue.insert(80);
while( !theQueue.isEmpty() ) // hapus dan tampilkan
{ // all items
long n = theQueue.remove(); // (
System.out.print(n);
System.out.print(“ “);
}
System.out.println(“”);
} // end main()
} // end class QueueApp
method insert()
Method insert() mengasumsikan bahwa queue tidak penuh (full). Kita tidak melihatnya dalam main(), tetapi kita bisa memanggil insert() hanya setelah memanggil isFull() dan memperoleh nilai kembalian yang salah. Pengisian data dengan cara menaikkan rear dan mengisikan data baru tersebut pada rear yang baru sekarang. Tetapi, jika rear berada di puncak array, pada maxSize-1, maka harus kembali ke posisi terbawah array sebelum penyisipan dilakukan. Caranya dengan memberi nilai rear=-1, sehingga jika terjadi kenaikan pada pada rear, maka rear akan menjadi 0, dasar dari array. Dan akhirnya, nItem bertambah.
Method remove()
Method remove mengasumsikan queue-nya tidak kosong. Untuk meyakinkan bahwa queue-nya tidak kosong, anda harus memanggil method isEmpty(). Penghapusan selalu dimulai dengan memperoleh nilai pada front dan kemudian mengurangi front. Jika front-nya terletak pada akhir array, maka harus kembali ke 0. Kemudian nItems dikurangi.
Method peek()
untuk mendapatkan nilai pada front.
Method isEmpty(), isFull(), and size()
untuk mengecek nItems, apakah kosong atau penuh.
Di dunia nyata apabila seseorang sedang mengantri (misalnya antri tiket kereta api), apabila telah dilayani dan memperoleh tiket, maka ia akan keluar dari antrian dan orang-orang yang berada di belakangnya akan bergerak maju ke dapan. Kita bisa saja menggerakkan setiap item data ke depan apabila kita menghapus data yang terdepan, tetapi hal ini kurang efektif. Sebaliknya kita tetap menjaga setiap item data di posisinya, yang kita lakukan hanyalah merubah posisi front dan rear saja.
Yang menjadi permasalahan adalah apabila posisi rear berada pada bagian akhir dari array (atau pada nomor indeks yang terbesar). Meskipun ada bagian yang kosong di awal-awal array – karena mungkin data telah dihapus, data baru tidak bisa dimasukkan lagi karena rear-nya sudah tidak bisa bergerak lagi. Atau mungkinkah posisi rear nya bisa berpindah? Situasi seperti itu bisa dilihat seperti gambar berikut:
circular queueUntuk menghindari permasalahan seperti itu (tidak bisa memasukkan data baru) – meskipun queue-nya belum penuh, maka front dan rear-nya berputar (kembali) ke bagian awal array. Kejadian seperti ini dinamakan dengan circular queue (atau kadang-kadang disebut juga dengan istilah ring buffer). Kejadian seperti ini seperti terlihat pada gambar berikut:
Berikut Contoh Implementasi Antrian dalam Java :
Queue.java
class Queue
{
private int maxSize;
private long[] queArray;
private int front;
private int rear;
private int nItems;
//————————————————————–
public Queue(int s) // konstruktor
{
maxSize = s;
queArray = new long[maxSize];
front = 0;
rear = -1;
nItems = 0;
}
//————————————————————–
public void insert(long j) // letakkan item (data) di posisi belakang dari queue
{
if(rear == maxSize-1) //
rear = -1;
queArray[++rear] = j; //naikkan rear dan masukkan item (data) pada posisi rear yang baru
nItems++; //tambah satu item lagi
}
//————————————————————–
public long remove() // hapus item (data) yang berada pada posisi front
{
long temp = queArray[front++]; //dapatkan nilainya dan naikkan front
if(front == maxSize) //
front = 0;
nItems–; // item (data) berkurang satu
return temp;
}
//————————————————————–
public long peekFront() //
{
return queArray[front];
}
//————————————————————–
public boolean isEmpty() //benar jika queue-nya kosong
{
return (nItems==0);
}
//————————————————————–
public boolean isFull() // benar jika queue-nya penuh
{
return (nItems==maxSize);
}
//————————————————————–
public int size() // jumlah ietm (data) dalam queue
{
return nItems;
}
//————————————————————–
} // end class Queue
QueueApp.java
class QueueApp
{
public static void main(String[] args)
{
Queue theQueue = new Queue(5); // queue menampung 5 item (data)
theQueue.insert(10); // masukkan 4 item (data)
theQueue.insert(20);
theQueue.insert(30);
theQueue.insert(40);
theQueue.remove(); // hapus 3 item (data)
theQueue.remove(); // (10, 20, 30)
theQueue.remove();
theQueue.insert(50); // masukkan 4 item (data) lagi
theQueue.insert(60); // (wraps around)
theQueue.insert(70);
theQueue.insert(80);
while( !theQueue.isEmpty() ) // hapus dan tampilkan
{ // all items
long n = theQueue.remove(); // (
System.out.print(n);
System.out.print(“ “);
}
System.out.println(“”);
} // end main()
} // end class QueueApp
method insert()
Method insert() mengasumsikan bahwa queue tidak penuh (full). Kita tidak melihatnya dalam main(), tetapi kita bisa memanggil insert() hanya setelah memanggil isFull() dan memperoleh nilai kembalian yang salah. Pengisian data dengan cara menaikkan rear dan mengisikan data baru tersebut pada rear yang baru sekarang. Tetapi, jika rear berada di puncak array, pada maxSize-1, maka harus kembali ke posisi terbawah array sebelum penyisipan dilakukan. Caranya dengan memberi nilai rear=-1, sehingga jika terjadi kenaikan pada pada rear, maka rear akan menjadi 0, dasar dari array. Dan akhirnya, nItem bertambah.
Method remove()
Method remove mengasumsikan queue-nya tidak kosong. Untuk meyakinkan bahwa queue-nya tidak kosong, anda harus memanggil method isEmpty(). Penghapusan selalu dimulai dengan memperoleh nilai pada front dan kemudian mengurangi front. Jika front-nya terletak pada akhir array, maka harus kembali ke 0. Kemudian nItems dikurangi.
Method peek()
untuk mendapatkan nilai pada front.
Method isEmpty(), isFull(), and size()
untuk mengecek nItems, apakah kosong atau penuh.
Struktur
Data Stack
Secara bahasa, Stack berarti
tumpukan. Jika dikaitkan dengan struktur data, Stack berarti sekumpulan data
yang organisasi atau strukturnya bersifat tumpukan atau menyerupai tumpukan.
Secara ilustrasi, stack dapat digambarkan dengan gambar di samping.
“Top “ merupakan pintu untuk keluar masuknya elemen – elemen stack. A, B, dan C merupakan suatukoleksi. Dari ilustrasi dapat digambarkan bahwa C merupakan elemen yang terakhir memasuki stack namunpertama keluar dari stack. Begitu sebaliknya dengan A. A merupakan elemen pertama yang memasukitumpukan namun terakhir saat keluar dari tumpukan.
Di dalam gambar juga terlihat urutan masuk dan keluar yang berkebalikan. Elemen yang masuk pertama akankeluar erakhir dan sebaliknya. Prinsip ini telah dikenal dalam struktur data dengan nama prinsip LIFO (Last In First Out).
Di dalam pengembangannya, stack dapat dikelompokkan menjadi dua bagian. Dua bagian tersebut yaitudan Double Stack. Single Stack
Single Stack
Single Stack atau Stack Tunggal adalah stack yang hanya terdiri dari satu koleksi. Bila stack inidirepresentasikan dengan array, maka pengisian dan penghapusan harus dilakukan bertahap dari indeksnya. TOP-
Di dalam proses single stack terdapat tiga macam proses utama, yaitu :
- Inisialisasi
- PUSH (Insert, Masuk, Simpan, Tulis)
- POP (Delete, Keluar, Ambil, Baca, Hapus)
INISIALISASI
Proses inisialisasi merupakan proses awal yang dilakukan untuk menyimpan indeks penunjuk stack. Roses inidilakukan dengan intruksi :
Secara ilustrasi, stack dapat digambarkan dengan gambar di samping.
“Top “ merupakan pintu untuk keluar masuknya elemen – elemen stack. A, B, dan C merupakan suatukoleksi. Dari ilustrasi dapat digambarkan bahwa C merupakan elemen yang terakhir memasuki stack namunpertama keluar dari stack. Begitu sebaliknya dengan A. A merupakan elemen pertama yang memasukitumpukan namun terakhir saat keluar dari tumpukan.
Di dalam gambar juga terlihat urutan masuk dan keluar yang berkebalikan. Elemen yang masuk pertama akankeluar erakhir dan sebaliknya. Prinsip ini telah dikenal dalam struktur data dengan nama prinsip LIFO (Last In First Out).
Di dalam pengembangannya, stack dapat dikelompokkan menjadi dua bagian. Dua bagian tersebut yaitudan Double Stack. Single Stack
Single Stack
Single Stack atau Stack Tunggal adalah stack yang hanya terdiri dari satu koleksi. Bila stack inidirepresentasikan dengan array, maka pengisian dan penghapusan harus dilakukan bertahap dari indeksnya. TOP-
Di dalam proses single stack terdapat tiga macam proses utama, yaitu :
- Inisialisasi
- PUSH (Insert, Masuk, Simpan, Tulis)
- POP (Delete, Keluar, Ambil, Baca, Hapus)
INISIALISASI
Proses inisialisasi merupakan proses awal yang dilakukan untuk menyimpan indeks penunjuk stack. Roses inidilakukan dengan intruksi :
top = -1;
|
PUSH
Proses push adalah proses memasukkan data baru ke stack indeks selanjutnya. Algoritma dasar proses PUSH adalah :
top = top + 1; array[top] =
variable_tampung;
|
POP
Proses pop adalah proses mengeluarkan / mengambil data dari stack dengan indeks yang disimpan padaAlgoritma dasar proses POP adalah : variable top.
variable_tampung = array[top]; top
= top – 1;
|
Double Stack
Double Stack atau Stack Ganda adalah stack yang hanya terdiri dari dua single stack. Bila stack inidirepresentasikan dengan array, maka pengisian dan penghapusan harus melalui salah satu arah.
Di dalam proses double stack terdapat lima macam proses utama, yaitu :
- Inisialisasi
- PUSH1 (Proses Push untuk Single Stack pertama)
- POP1 (Proses Pop untuk Single Stack pertama)
- PUSH2 (Proses Push untuk Single Stack kedua)
- POP2 (Proses Pop untuk Single Stack kedua)
Algoritma dasar masing – masing proses adalah sebagai berikut :
INISIALISASI
|
top1 = -1; top2 = MAX_ARRAY;
|
PUSH1
|
top1 = top1 + 1; array[top1] = variable_tampung;
|
POP1
|
variable_tampung = array[top1]; top1 = top1 – 1;
|
PUSH2
|
top2 = top2 – 1; array[top2] = variable_tampung;
|
POP2
|
variable_tampung = array[top2];
top2 = top2 + 1;
|
STRUKTUR
DATA GRAPH
Graph
merupakan struktur data yang paling umum. Jika struktur linear memungkinkan
pendefinisian keterhubungan sikuensial antara entitas data, struktur data tree
memungkinkan pendefinisian keterhubungan hirarkis, maka struktur graph
memungkinkan pendefinisian keterhubungan tak terbatas antara entitas data.
Banyak entitas-entitas data dalam masalah-masalah nyata secara alamiah memiliki keterhubungan langsung (adjacency) secara tak terbatas demikian. Contoh: informasi topologi dan jarak antar kota-kota di pulau Jawa. Dalam masalah ini kota x bisa berhubungan langsung dengan hanya satu atau limaentitas-entitas data dalam masalah-masalah nyata secara alamiah memiliki keterhubungan langsung (adjacency) secara tak terbatas demikian. Contoh: informasi topologi dan jarak antar kota-kota di pulau Jawa. Dalam masalah ini kota x bisa berhubungan langsung dengan hanya satu atau lima kota lainnya. Untuk memeriksa keterhubungan dan jarak tidak langsung antara dua kota dapat diperoleh berdasarkan data keterhubungan-keterhubungan langsung dari kota-kota lainnya yang memperantarainya.
Representasi data dengan struktur data linear ataupun hirarkis pada masalah ini masih bisa digunakan namun akan membutuhkan pencarian-pencarian yang kurang efisien. Struktur data graph secara eksplisit menyatakan keterhubungan ini sehingga pencariannya langsung (straightforward) dilakukan pada strukturnya sendiri.
Masalah-masalah Graph
Masalah path minimum (Shortest path problem):
mencari route dengan jarak terpendek dalam suatu jaringan transportasi.
Masalah aliran maksimum (maximum flow problem):
menghitung volume aliran BBM dari suatu reservoir ke suatu titik tujuan melalui jaringan pipa.
Masalah pencariah dalam graph (graph searching problem):
mencari langkah-langkah terbaik dalam program permainan catur komputer.
Masalah pengurutan topologis (topological ordering problem):
menentukan urutan pengambilan mata-mata kuliah yang saling berkaitan dalam hubungan prasyarat (prerequisite).
Masalah jaringan tugas (Task Network Problem):
membuat penjadwalan pengerjaan suatu proyek yang memungkinkan waktu penyelesaian tersingkat.
Masalah pencarian pohon rentang minimum (Minimum Spanning Tree Problem):
mencari rentangan kabel listrik yang totalnya adalah minimal untuk menghubungkan sejumlah kota.
Travelling Salesperson Problem:
tukang pos mencari lintasan terpendek melalui semua alamat penerima pos tanpa harus mendatangi suatu tempat lebih dari satu kali.
Four-color problem:
dalam menggambar peta, memberikan warna yang berbeda pada setiap propinsi yang saling bersebelahan.
Definisi
Suatu graph didefinisikan oleh himpunan verteks dan himpunan sisi (edge). Verteks menyatakan entitas-entitas data dan sisi menyatakan keterhubungan antara verteks. Biasanya untuk suatu graph G digunakan notasi matematis
G = (V, E)
V adalah himpunan verteks dan E himpunan sisi yang terdefinisi antara pasangan-pasangan verteks. Sebuah sisi antara verteks x dan y ditulis {x, y}.
Suatu graph H = (V1, E1) disebut subgraph dari graph G jika V1 adalah himpunan bagian dari V dan E1 himpunan bagian dari E.
Digraph & Undigraph
Graph Berarah (directed graph atau digraph): jika sisi-sisi pada graph, misalnya {x, y} hanya berlaku pada arah-arah tertentu saja, yaitu dari x ke y tapi tidak dari y ke x; verteks x disebut origin dan vertex y disebut terminus dari sisi tersebut. Secara grafis maka penggambaran arah sisi-sisi digraph dinyatakan dengan anak panah yang mengarah ke verteks terminus, secara notasional sisi graph berarah ditulis sebagai vektor dengan (x, y).
graph di samping ini adalah suatu contoh Digraph G = {V, E}
dengan V = {A, B, C, D, E, F, G, H, I,J, K, L, M}
dan E = {( (A,B),(A,C), (A,D), (A,F), (B,C), (B,H), (C,E), (C,G), (C,H), (C,I), (D,E), (D,F), (D,G), (D,K), (D,L), (E,F), (G,I), (G,K), (H,I), (I,J), (I,M), (J,K), (J,M), (L,K), (L,M)}.
Graph Tak Berarah (undirected graph atau undigraph): setiap sisi {x, y} berlaku pada kedua arah: baik x ke y maupun y ke x. Secara grafis sisi pada undigraph tidak memiliki mata panah dan secara notasional menggunakan kurung kurawal.
graph di samping ini adalah suatu contoh Undigraph G = {V, E}
dengan V = {A, B, C, D, E, F, G, H, I,J, K, L, M}
dan E = { {A,B},{A,C}, {A,D}, {A,F}, {B,C}, {B,H}, {C,E}, {C,G}, {C,H}, {C,I}, {D,E}, {D,F}, {D,G}, {D,K}, {D,L}, {E,F}, {G,I}, {G,K}, {H,I}, {I,J}, {I,M}, {J,K}, {J,M}, {L,K}, {L,M}}.
Dalam masalah-masalah graph undigraph bisa dipandang sebagai suatu digraph dengan mengganti setiap sisi tak berarahnya dengan dua sisi untuk masing-masing arah yang berlawanan.
Undigraph di atas tersebut bisa dipandang sebagai Digraph G = {V, E}
dengan V = {A, B, C, D, E, F, G, H, I,J, K, L, M}
dan E = { (A,B),(A,C), (A,D), (A,F), (B,C), (B,H), (C,E), (C,G), (C,H), (C,I), (D,E), (D,F), (D,G), (D,K), (D,L), (E,F), (G,I), (G,K), (H,I), (I,J), (I,M), (J,K), (J,M), (L,K), (L,M), (B,A), (C,A), (D,A), (F,A), (C,B), (H,B), (E,C), (G,C), (H,C), (I,C), (E,D), (F,D), (G,D), (K,D), (L,D), (F,E), (I,G), (K,G), (I,H), (J,I), (M,I), (K,J), (M,J), (K,L), (M,L)}
Selain itu, berdasarkan definisi ini maka struktur data linear maupun hirarkis adalah juga graph. Node-node pada struktur linear atupun hirarkis adalah verteks-verteks dalam pengertian graph dengan sisi-sisinya menyusun node-node tersebut secara linear atau hirarkis. Sementara kita telah ketahui bahwa struktur data linear adalah juga tree dengan pencabangan pada setiap node hanya satu atau tidak ada. Linear 1-way linked list adalah digraph, linear 2-way linked list bisa disebut undigraph.
Banyak entitas-entitas data dalam masalah-masalah nyata secara alamiah memiliki keterhubungan langsung (adjacency) secara tak terbatas demikian. Contoh: informasi topologi dan jarak antar kota-kota di pulau Jawa. Dalam masalah ini kota x bisa berhubungan langsung dengan hanya satu atau limaentitas-entitas data dalam masalah-masalah nyata secara alamiah memiliki keterhubungan langsung (adjacency) secara tak terbatas demikian. Contoh: informasi topologi dan jarak antar kota-kota di pulau Jawa. Dalam masalah ini kota x bisa berhubungan langsung dengan hanya satu atau lima kota lainnya. Untuk memeriksa keterhubungan dan jarak tidak langsung antara dua kota dapat diperoleh berdasarkan data keterhubungan-keterhubungan langsung dari kota-kota lainnya yang memperantarainya.
Representasi data dengan struktur data linear ataupun hirarkis pada masalah ini masih bisa digunakan namun akan membutuhkan pencarian-pencarian yang kurang efisien. Struktur data graph secara eksplisit menyatakan keterhubungan ini sehingga pencariannya langsung (straightforward) dilakukan pada strukturnya sendiri.
Masalah-masalah Graph
Masalah path minimum (Shortest path problem):
mencari route dengan jarak terpendek dalam suatu jaringan transportasi.
Masalah aliran maksimum (maximum flow problem):
menghitung volume aliran BBM dari suatu reservoir ke suatu titik tujuan melalui jaringan pipa.
Masalah pencariah dalam graph (graph searching problem):
mencari langkah-langkah terbaik dalam program permainan catur komputer.
Masalah pengurutan topologis (topological ordering problem):
menentukan urutan pengambilan mata-mata kuliah yang saling berkaitan dalam hubungan prasyarat (prerequisite).
Masalah jaringan tugas (Task Network Problem):
membuat penjadwalan pengerjaan suatu proyek yang memungkinkan waktu penyelesaian tersingkat.
Masalah pencarian pohon rentang minimum (Minimum Spanning Tree Problem):
mencari rentangan kabel listrik yang totalnya adalah minimal untuk menghubungkan sejumlah kota.
Travelling Salesperson Problem:
tukang pos mencari lintasan terpendek melalui semua alamat penerima pos tanpa harus mendatangi suatu tempat lebih dari satu kali.
Four-color problem:
dalam menggambar peta, memberikan warna yang berbeda pada setiap propinsi yang saling bersebelahan.
Definisi
Suatu graph didefinisikan oleh himpunan verteks dan himpunan sisi (edge). Verteks menyatakan entitas-entitas data dan sisi menyatakan keterhubungan antara verteks. Biasanya untuk suatu graph G digunakan notasi matematis
G = (V, E)
V adalah himpunan verteks dan E himpunan sisi yang terdefinisi antara pasangan-pasangan verteks. Sebuah sisi antara verteks x dan y ditulis {x, y}.
Suatu graph H = (V1, E1) disebut subgraph dari graph G jika V1 adalah himpunan bagian dari V dan E1 himpunan bagian dari E.
Digraph & Undigraph
Graph Berarah (directed graph atau digraph): jika sisi-sisi pada graph, misalnya {x, y} hanya berlaku pada arah-arah tertentu saja, yaitu dari x ke y tapi tidak dari y ke x; verteks x disebut origin dan vertex y disebut terminus dari sisi tersebut. Secara grafis maka penggambaran arah sisi-sisi digraph dinyatakan dengan anak panah yang mengarah ke verteks terminus, secara notasional sisi graph berarah ditulis sebagai vektor dengan (x, y).
graph di samping ini adalah suatu contoh Digraph G = {V, E}
dengan V = {A, B, C, D, E, F, G, H, I,J, K, L, M}
dan E = {( (A,B),(A,C), (A,D), (A,F), (B,C), (B,H), (C,E), (C,G), (C,H), (C,I), (D,E), (D,F), (D,G), (D,K), (D,L), (E,F), (G,I), (G,K), (H,I), (I,J), (I,M), (J,K), (J,M), (L,K), (L,M)}.
Graph Tak Berarah (undirected graph atau undigraph): setiap sisi {x, y} berlaku pada kedua arah: baik x ke y maupun y ke x. Secara grafis sisi pada undigraph tidak memiliki mata panah dan secara notasional menggunakan kurung kurawal.
graph di samping ini adalah suatu contoh Undigraph G = {V, E}
dengan V = {A, B, C, D, E, F, G, H, I,J, K, L, M}
dan E = { {A,B},{A,C}, {A,D}, {A,F}, {B,C}, {B,H}, {C,E}, {C,G}, {C,H}, {C,I}, {D,E}, {D,F}, {D,G}, {D,K}, {D,L}, {E,F}, {G,I}, {G,K}, {H,I}, {I,J}, {I,M}, {J,K}, {J,M}, {L,K}, {L,M}}.
Dalam masalah-masalah graph undigraph bisa dipandang sebagai suatu digraph dengan mengganti setiap sisi tak berarahnya dengan dua sisi untuk masing-masing arah yang berlawanan.
Undigraph di atas tersebut bisa dipandang sebagai Digraph G = {V, E}
dengan V = {A, B, C, D, E, F, G, H, I,J, K, L, M}
dan E = { (A,B),(A,C), (A,D), (A,F), (B,C), (B,H), (C,E), (C,G), (C,H), (C,I), (D,E), (D,F), (D,G), (D,K), (D,L), (E,F), (G,I), (G,K), (H,I), (I,J), (I,M), (J,K), (J,M), (L,K), (L,M), (B,A), (C,A), (D,A), (F,A), (C,B), (H,B), (E,C), (G,C), (H,C), (I,C), (E,D), (F,D), (G,D), (K,D), (L,D), (F,E), (I,G), (K,G), (I,H), (J,I), (M,I), (K,J), (M,J), (K,L), (M,L)}
Selain itu, berdasarkan definisi ini maka struktur data linear maupun hirarkis adalah juga graph. Node-node pada struktur linear atupun hirarkis adalah verteks-verteks dalam pengertian graph dengan sisi-sisinya menyusun node-node tersebut secara linear atau hirarkis. Sementara kita telah ketahui bahwa struktur data linear adalah juga tree dengan pencabangan pada setiap node hanya satu atau tidak ada. Linear 1-way linked list adalah digraph, linear 2-way linked list bisa disebut undigraph.
Pengertian
Struktur Data Linked List
Linked list (list bertaut) adalah
salah satu struktur data dasar yang sangat fundamental dalam bidang ilmu
komputer. Dengan menggunakan linked list maka programmer dapat menimpan datanya
kapanpun dibutuhkan. Linked list mirip dangan array, kecuali pada linked list
data yang ingin disimpan dapat dialokasikan secara dinamis pada saat
pengoperasian program (run-time).
Pada array, apabila programmer ingin menyimpan data, programmer diharuskan untuk mendefinisikan besar array terlebih dahulu, seringkali programmer mengalokasikan array yang sangat besar(misal 100). Hal ini tidak efektif karena seringkali yang dipakai tidak sebesar itu. Dan apabila programmer ingin menyimpan data lebih dari seratus data, maka hal itu tidak dapat dimungkinkan karena sifat array yang besarnya statik. Linked list adalah salah satu struktur data yang mampu menutupi kelemahan tersebut.
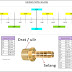
Secara umum linked list tersusun atas sejumlah bagian-bagian data yang lebih kecil yang terhubung (biasanya melalui pointer). Linked list dapat divisualisasikan seperti kereta, bagian kepala linked list adalah mesin kereta, data yang disimpan adalah gerbong, dan pengait antar gerbong adalah pointer.
-------- -------- --------
Mesin Data Data
-------- -------- --------
(kepala) ---> Pointer ---> Pointer --
-------- -------- --------
Programmer membaca data menyerupai kondektur yang ingin memeriksa karcis penumpang. Programmer menyusuri linked list melalui kepalanya, dan kemudian berlanjut ke gerbong (data) berikutnya, dan seterusnya sampai gerbong terakhir (biasanya ditandai dengan pointer menunjukkan alamat kosong (NULL)). Penyusuran data dilakukan secara satu persatu sehingga penyusuran data bekerja dengan keefektifan On. Dibandingkan array, ini merupakan kelemahan terbesar linked list. Pada array, apabilan programmer ingin mengakses data ke-n (index n), maka programmer dapat langsung mengaksesnya. Sedangkan dengan linked list programmer harus menyusuri data sebanyak n terlebih dahulu.
Pada array, apabila programmer ingin menyimpan data, programmer diharuskan untuk mendefinisikan besar array terlebih dahulu, seringkali programmer mengalokasikan array yang sangat besar(misal 100). Hal ini tidak efektif karena seringkali yang dipakai tidak sebesar itu. Dan apabila programmer ingin menyimpan data lebih dari seratus data, maka hal itu tidak dapat dimungkinkan karena sifat array yang besarnya statik. Linked list adalah salah satu struktur data yang mampu menutupi kelemahan tersebut.
Secara umum linked list tersusun atas sejumlah bagian-bagian data yang lebih kecil yang terhubung (biasanya melalui pointer). Linked list dapat divisualisasikan seperti kereta, bagian kepala linked list adalah mesin kereta, data yang disimpan adalah gerbong, dan pengait antar gerbong adalah pointer.
-------- -------- --------
Mesin Data Data
-------- -------- --------
(kepala) ---> Pointer ---> Pointer --
-------- -------- --------
Programmer membaca data menyerupai kondektur yang ingin memeriksa karcis penumpang. Programmer menyusuri linked list melalui kepalanya, dan kemudian berlanjut ke gerbong (data) berikutnya, dan seterusnya sampai gerbong terakhir (biasanya ditandai dengan pointer menunjukkan alamat kosong (NULL)). Penyusuran data dilakukan secara satu persatu sehingga penyusuran data bekerja dengan keefektifan On. Dibandingkan array, ini merupakan kelemahan terbesar linked list. Pada array, apabilan programmer ingin mengakses data ke-n (index n), maka programmer dapat langsung mengaksesnya. Sedangkan dengan linked list programmer harus menyusuri data sebanyak n terlebih dahulu.
STRUTUR DATA SORT
Sort adalah proses
pengurutan data yang sebelumnya disusun secara acak sehingga menjadi tersusun
secara teratur menurut suatu aturan tertentu.
Pada umumnya terdapat 2
jenis pengurutan :
v Ascending (Naik)
v Descending (Turun)
Contoh :
Data Acak : 5 6 8 1 3 25
10
Terurut Ascending : 1 3
5 6 8 10 25
Terurut Descending : 25
10 8 6 5 3 1
Untuk melakukan proses
pengurutan tersebut dapat digunakan berbagai macam cara / metoda. Beberapa
metoda diantaranya :
a) Buble / Exchange Sort
b) Selection Sort
c) Insertion Sort
d) Quick Sort
Bubble / Exchange Sort
Memindahkan elemen yang
sekanag dengan elemen yang berikutnya, jika elemen sekarang > elemen
berikutnya, maka tukar
Proses :
22 10 15 3 8 2
22 10 15 3 2 8
22 10 15 2 3 8
22 10 2 15 3 8
22 2 10 15 3 8
2 22 10 15 3 8
Langkah 1 :
Pengecekan dapat dimulai
dari data paling awal atau paling akhir. Pada contoh di samping ini pengecekan
di mulai dari data yang paling akhir. Data paling akhir dibandingkan dengan
data di depannya, jika ternyata lebih kecil maka tukar. Dan pengecekan yang
sama dilakukan terhadap data yang selanjutnya sampai dengan data yang paling
awal.
Langkah 2 :
Proses di atas adalah
pengurutan data dengan metoda bubble ascending.
Untuk yang descending
adalah kebalikan dari proses diatas.
Berikut penggalan
listing program Procedure TukarData dan Procedure Bubble Sort.
Procedure TukarData
Procedure TukarData(var
a,b : word);
Var c : word;
Begin
c:=a;
a:=b;
b:=c;
end;
Procedure Bubble Sort
Ascending
Procedure Asc_Bubble(var
data:array; jmldata:integer);
Var i,j : integer;
Begin
For i:= 2 to jmldata do
For j:= jmldata downto I
do
If data[j] <>
Tukardata (data[j],
data[j-1]);
end;
Untuk pengurutan secara
descending anda hanya perlu menggantikan baris ke-6 dengan berikut ini :
If data[j] >
data[j-1] then
Selection Sort
Membandingkan elemen
yang sekarang dengan elemen yang berikutnya sampai dengan elemen yang terakhir.
Jika ditemukan elemen lain yang lebih kecil dari elemen sekarang maka dicatat
posisinya dan kemudian ditukar. Dan begitu seterusnya.








0 komentar: